The Possibility of the Impossible
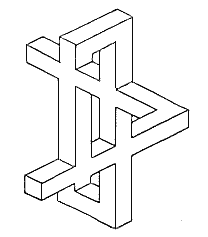 |
There is something
odd about this drawing - an impossibility, if you like.
But if you look at a sufficiently small region of it, the
oddness disappears. You cannot say that the impossibility
is here, or here - it is something about the global
structure. Roger Penrose at the Lund conference on Parts and Wholes, in 1983. |
| Perspective japonaise no 264 |
The Swedish artist Oskar Reutersvärd has made a series of drawings under the common title "perspective japonaise". They show us seemingly three-dimensional objects which on closer scrutiny are found to be "impossible". An example is shown above. Of course you could look upon these drawings just as a good joke. But the drawings - like the well-known pictures of Escher - bring up a question of far-reaching importance: Exactly what do we mean when we say that a fictitious object is "impossible"? The first reaction would be to regard the Reutersvärd pictures as optical illusions. After all, we are spontaneously interpreting a drawing on a flat surface as representing a three-dimensional solid object. This, however, is only due to our perceptual habits. The picture could as well represent, say, a flat sculpture made of metal wires. The depth we perceive in a picture is always illusory. But what then? I would not say this is the essential point in discussing these drawings.
The most challenging question is not whether the pictures may be 'explained' in terms of what we know about visual perception, but rather, what such pictures, deliberately regarded as representations, can reveal to us. If we accept what we see - what do the pictures tell us; what kind of reality do the depicted objects have? And, again, what makes us call them "impossible"?
In fact, this is not quite as trivial a question as it might seem. Let me render it more incisive. How do we know that the object represented on the drawing cannot exist? - Is it because we have never seen a body of that particular shape? No, it is not merely a question of what we are accustomed to seeing. We feel sure that we will not some day come across an object of this odd shape. Nor is it a logical conclusion, since who is prepared to state on the spot the axiomatic premises from which such a conclusion could be drawn? But if it is neither an empirical fact nor a theoretical conclusion - what is it? I would suggest that it is a practical conclusion. We just cannot imagine how to make such an object.
I mean, suppose we regard the drawing as a design for an object to be fabricated, say, out of pear-wood. And let us try to realize it.
We start by making a number of straight, square beams. Then we put them together, one after the other, starting somewhere in the structure, following the drawing. To begin with, it works well enough. But very soon you find that you cannot manage to join two ends that should be joined according to the drawing. The object cannot be finished, you have to leave it "open". If you start anew, putting beams together in another order this time, you will sooner or later get stuck again. In this way you get a number of unfinished objects. It seems as if the impossibility at issue is the impossibility of making one uniquely connected object, as shown on the drawing. (In a way you could say the drawn object is a `synthesis' of a number of related possible objects.)
The paradox is, however, that if you consider a sufficiently small region of the drawing the oddness disappears. That is to say, the `impossibility' is not here, or here - it is something about the object as a whole.
Nothing is wrong with the beams that make up the structure, nor with the way two beams are joined together orthogonally to each other. Locally the object is quite all right. But the local consistency of the structure does not guarantee the consistency of the whole of it.
But does not this give you an uneasy feeling? I am afraid that we usually design complex structures just by putting well-established facts together in a clever way, and relying on `continuity' to secure the feasibility of the whole.
At least this seems to be the way our bureaucrats try to organize society. In our desperate efforts simultaneously to follow all rules that together should make our society perfectly organized, we probably look like people trying to put together one of Reutersvärd's impossible structures!
In the case of a Reutersvärd drawing you can without much difficulty directly `see' whether it will do as an ordinary three-dimensional body or not. But suppose we invent a complicated system, made up of parts or subroutines, that are in perfect condition taken by themselves, and which are interconnected in a reasonable way, we still cannot be sure that the structure as a whole in reality will not turn out to be nonsensical. I think some people's ingenious designs for a perpetuum mobile belongs here (and by the way one of Escher's famous pictures shows us one!).
Moreover, is this not the way we scientists make up our `world picture' - each research worker contributing his straw to the big anthill? But if local consistency does not guarantee the consistency of the whole....
So what hope do we have that our scientific world picture is not an impossible drawing, like the Reutersvärd ones?
Now, to put it in more general terms, let us regard Reutersvärd's axonometric drawings as a kind of `picture language'. Any `sentence' in this language is constructed in strict adherence to a set of rules, that is to say, a simple grammar. Each sentence can be interpreted as a `proposition', i.e. a suggested design for any of the three-dimensional objects that the language `is about'. Some propositions are semantically true, others false. To be able to distinguish the `true' designs from the `false' ones you have to take a position `outside' the picture language, since you must know what the symbolic constructions `are about'. In complicated cases, it may not be until you put a proposition to practical test that you find that it tells sheer nonsense.
If you are a pupil learning the noble craft of making axonometric perspective drawings, and you happen to draw an `impossible' figure, your teacher would tell you: "No, this is wrong, you are not allowed to draw these lines here, you see". In this way the pupil develops a skill to avoid making `wrong' pictures. But in the case of very complicated structures, he would still, at some rare occasions, make a mistake and draw an impossible connection. Would it not be better to include among the rules of the axonometric perspective a rule to prevent the drawing of non-permissible connections? Well, the problem is that in order to apply such a rule you must refer to the drawer's idea about what kind of object he is drawing. i.e. which one of all possible figures he intends to represent. So it cannot be a formal rule within the grammar of the axonometric perspective. All pictures are formally correct. The settlement, whether a drawing is `true' or not, must be done on the level of a meta-language, which comprises the interpretation of the sentences of the picture language.
To formalize such a meta-language would be quite a tedious procedure, I am afraid. It must include the axioms for some kind of `space' in which the structures extend themselves, and where the terminal points of beams can meet - or not meet, as the case may be.
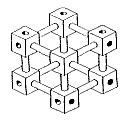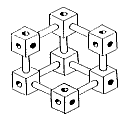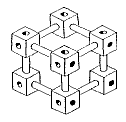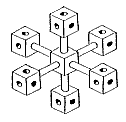
Out of cubiform nuts and connecting rods you can build various objects. Try to build the object shown in this drawing!
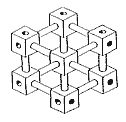
You will soon find that it is impossible to put nuts and rods together in this peculiar way, without bending them. But the following drawing represent objects possible to build.
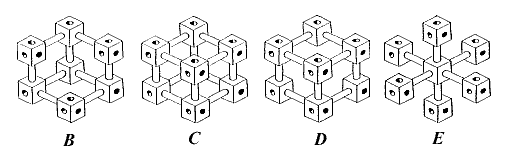
The impossible one, call it A, is a kind of `synthesis' of all four B - E. To prevent the drawing of an impossible object, which connections should be forbidden? In fact, any line in A must be permissible, since it appears in some or other of the possible figures B - E. If you do not know which one of B, C, D, E is intended you cannot tell a priori which line connections should be forbidden and which not.
*
If you asked Reutersvärd when drawing one of his figures: "What do you intend to represent in this drawing?" he would answer "I don't know. I am just making one of my pictures, following the rules of the `perspective japonaise'. Let's see what comes out". Thus, it cannot be said that the Reutersvärd drawings are wrong or that they do not make sense. It is only that they do not refer to anything - at least not in our ordinary world of tables and chairs.
For comparison consider the well-known creature called centaur. It is half human being, half horse, and has been depicted countless times. So the word certainly has a meaning, although the creature in question does only have a mythological existence. Let us permit ourselves to speculate freely about what the challenging drawings of Reutersvärd could possibly refer to! First, suppose the drawing above shows the result of the mapping of a huge object that we explore by moving about on it. Without our observing it, the object changes its shape in the course of our investigation. So far, we have taken it for granted that Reutersvärd's pictures represent synchronous slices of space-time. But who says an artist must act like a camera? And who says he must show us ordinary, rigid bodies of invariable shape?
Secondly, I observe that some of the `impossible' objects make one think of the world of atoms and molecules. Now, as a matter of fact, the relation between the whole and its parts turns out to be rather paradoxical at the molecular level, if quantum mechanics is taken for granted. A fundamental principle in quantum mechanics states that any superposition of observable states of a system is to be regarded as a possible state of the system as well. In discussing the structure of molecules and the nature of the chemical bond, the phenomenon of mesomerism means that the actual electron distribution must be conceived as lying somewhere "between" the electron distributions implied by the limiting formulae, the so called canonical structures, which are possible to illustrate by concrete models on the macroscopic level.
On the other hand, a so called `impossible object' might be looked upon as a `superposition' of a number of possible objects (i.e. the various configurations you arrive at in trying to assemble the impossible one!) So, maybe, Reutersvärd shows us a world of quantum-mechanically indeterminate objects - the possibility of the impossible!
 |
© Pehr Sällström, 2006 (Originally in Cybernetics and Human knowing Vol.1, No 2, 1992)
To be found at http://pscolour.eu/English/impossible.htm