How can red plus green make yellow?

Question

By adding the three primaries of a computer screen in various proportions all hues should be obtainable. The primaries are red (R), green (G) and blue (B). It is obvious that R and B can give bluered hues, such as violet, magenta, purple. It is also obvious that G and B can give turquoise, which is a bluegreen hue. But how can R and G give yellow? Yellow is not sensed as a ”greenred” or "redgreen" hue.

Answer

It is not as mysterious as it might seem. By closer scrutiny you will find that R is a yellow-red colour, and that G is a yellow-green colour. So, when these lights are added together the red and the green aspects of the colours balance out each other, being incompatible. What we see is the remaining yellow. It was there already from the beginning, so to speak!

You can nicely demonstrate this on your data screen with a suitable computer program. First you show the pure primaries R and G, overlapping to make Y (yellow). Then you add into R a suitable amount of the primary B to make it look ”just red”, i.e. a red which tends neither to yellow nor to blue. Likewise, you add into G such an amount of B that it looks neither yellow-green nor blue-green, but ”just green”. (Se illustration below) Then the two colour fields do not any longer add to make yellow, but rather white. They are complementary. The hues neutralize each other, with an achromatic result.

At least, so it is according to the opponent colours theory. Empirically it is not perfectly, only approximately true – but it is a sufficiently close approximation to be enlightening and useful!

Afterthoughts in December 2015

Some people have commented: "I see no problem in accepting that red plus green makes yellow". That yellow light can be obtained by superimposing red light and green light is an easily demonstrated fact -- and also quite reasonable, since they are neighbouring colours in the spectrum.

Let me however give some reasons why this could still be regarded an intriguing fact, after all.

(1) Two kinds of colour mixing

If you are an experienced painter, for instance from working with water colours, you know that you must have access to yellow as a primary colour. You cannot produce it by mixing others. Definitely not from red and green. And you don't need green as a primary, since it can be produced by mixing yellow with blue. White, yellow, blue and red are sufficient as a mini-set of primary colours. More precisely it should be yellow, cyan and magenta. So that cyan and magenta could give you a deep blue and yellow and magenta a warm red colour.

These rules are true for so called "subtractive colour mixing", dealing with material substances. But in my note above we are speaking of additive mixing, dealing with coloured lights. As on a computer screen. This kind of mixing follows other rules and uses other primaries. Yellow is not needed as primary, since it can be obtained by a combination of red and green, suitably choiced. Namely as orange-red and yellowish green. As seen in the illustration above.

I remember from a course, where the pupils were given an opportunity to look through a handy microscope with 25X magnification at a yellow area on a LCD screen. One of the pupils was terribly disappointed. On closer scrutiny there was no yellow on the screen, only green and red dots. The yellow was faked, an illusion, produced by a durty trick. She emphatically declared that she would never look at colour pictures on a computer screen any more.

The idea that yellow is a pure colour, not secondarily produced as mixed, is deeply rooted. It is as with white, which is not experienced as a mixture of R, G and B. Although you know that it actually is produced that way on the screen.

My point with the initial query was actually the following: In case of additive mixing (superimposing lights) you can always see on the two components what the result of adding them will be. This is not the case for "subtractive" mixing, that is, when you are mixing pigments or colorants or putting colour transparencies onto each other.

For instance combining a yellow and a blue filter to get a green one. This is true as a rule of thumb, but which filter combination would result in the best green, the most brilliant and saturated green, you cannot tell from how the two filters look separately. They have invisible secrets. You have to know the spectral distributions of the filters, in order to be able to predict the result of combining them. Or, alternatively, have experience of the specific colour material you use, how it behaves under various light sources etc. This kind of knowledge from further investigation is not necessary in the case of additive mixing of light stimuli. (Since the hue attribute of a light is distributive on superposition of lights.)

This might seem as a technical petitess, but it makes it much easier to work with colour on a computer screen than on a colour printer.

(2) Unique hues

When Ewald Hering in 1874 presented what he called "Das natürliche System der Farbenempfindungen" (The natural colour system), based on careful study of serial arrangements of colours according to hue, he pointed out an interesting fact. We find it natural to describe any particular hue with reference to two out of four reference hues: yellow, blue, red, green. That is to say, orange can be called yellowred. Violet can be called bluered, cyan can be called bluegreen and so on. But the four reference hues are exceptions. They are singular, or unique. You cannot (in the same obvious sense) describe yellow as redgreen. Nor green as yellowblue.

The four unique hues are points of transition: Unique yellow is a yellow that is neither greenish nor reddish yellow. Unique green is a green that is neither yellowish green, nor blueish green. And likewise for unique red and unique blue.

Furthermore the unique colours are pairwise opponent. Red to Green and Yellow to Blue. Opponent colours are suitably placed diametrically opposed to each other on the hue circle, with white at the center.

And the R-G pair is completely independent of the Y-B pair. Unique blue cannot be described as a red-green colour. Nor can unique yellow be described as a red-green colour.

This is how a hue circle a la Hering is often illustrated:

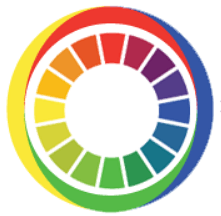
So when we carelessly say that on a computer screen "red plus green makes yellow" this seems to be a statement contradicting the phenomenological experience. It cannot be true, if we mean unique red and unique green. Since they are opponent, they would rather neutralize each other and add to white (or an achromatic grey).

The only possibility for the statement to be true seems to be if one adds a yellowred and a yellowgreen light, to be found on the left side in the diagram above. Then the redness and greeness, being opponent tendencies, should neutralize each other and the common yellow attribute remain. Observe that I am now speaking about the hue attribute of the light fluxes involved, not of their spectral distributions.

(3) Habits and preferences

Maybe we have become so used to the red and green on our digital screens (TV, mobile phones, surfpads, computers, cameras) that we regard them as just red and green, and not particularly as orangered and yellowgreen.


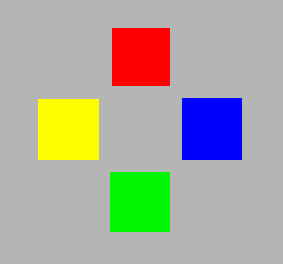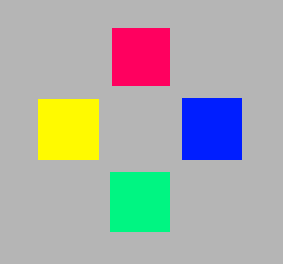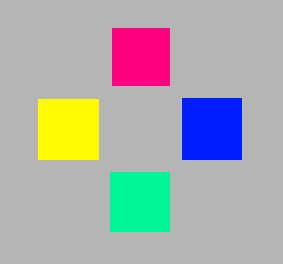Standard RGB	Unique hues	Pehaps too far

It must be held in mind that Hering is speaking of the hue attribute of colour perception. Unique red is not necessarily the "best" red or most impressive or most typical red. Because that depends on other aspects, such as saturation, brightness etc.

This is particularly true as concerns green. In practice it is very difficult to judge exactly where the position of unique green should be in a spectrum. Most observers tend to prefer a slightly yellowish green, as being "typical green". It is easier to indicate the position of unique yellow. And whether there is a unique red to be found in the spectrum, or if all long wavelengths have a slight yellow tint, is disputed. According to Hering a unique red can only be obtained by mixing the two ends of the spectrum in suitable proportion.

(4) Colorimetric evidence

So far the basic hue aspects, "yellowness", "blueness", "redness" and "greeness" are qualitative judgements. Could there be a material basis for this purely subjective experience? Hering, who was a physiologist, suggested opponent processes at the neural level in the retina.

Since I am a physicist I prefer serching for a more formal answer, in colorimetry. And (alas!) there is one. It was pointed out by Erwin Schrödinger in 1925 that it is possible mathematically to join the standard trichromatic colour model with an opponent-colours model. And this possibility has since been explored by others.

The radiation detected at the retinal level is measured by the eye as to its yellow/blue chromatic valency and to its red/green chromatic valency. The measurement can be described mathematically as an integral over the spectral range of the spectral distribution, weighted by the following two functions:

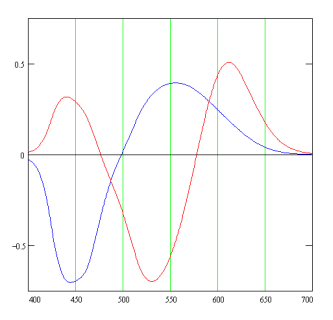
Positiv values of the red curve represent red, negative values green. Positive values of the blue curve represent yellow, negative blue. So the point where yellowness shifts into blueness is at 500 nm. (Which, on a frequency scale, would mean at the middle of the spectrum.)

The chromaticity diagram is divided into 4 parts: the yellow-green, the yellow-red, the blue-red and the blue-green lights. The dividing lines are defined by the positions of the unique yellow, unique blue and unique green in the spectrum, together with the white-point at the center (which helps to define the position of unique red on the purple line.)

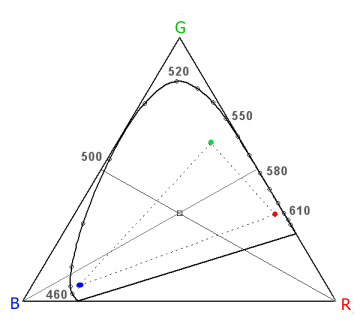
As you see from this diagram, unique red corresponds to the virtual red, at the right corner of the triangle RGB, spanning the colour mathcing system. This R probably corresponds to the respons of the long-wave sensitive cones. (The reason why the three corners are virtual colours (not physically realizable) is that the spectral sensitivity curves of the three retinal cone types are overlapping. For any kind of physical light, even purely monochromatic light, they are always stimulated in combinations.)

It is evident that the balance point between R and G is Yellow, not White. But the balance point between Yellow and Blue is White. R is balanced through White by a green colour that is not yellowgreen, as G, but halfways to Blue.

The full drawn curve (with some indicated wavelength positions) encloses the possible physical light stimuli. The dotted lines enclose the gamut area of the sRGB colour reproduction system.