FORMALIZATION AND INVENTION
BACKGROUND
During a couple of years I was deeply involved in a study of the use of symbolic notation in various disciplines, such as mathematics, music, dance (choreography), cartography, chemistry, physics, architecture. This resulted, in 1991, in the book "Tecken att tänka med" (Thinking by help of signs). I was asked to present my findings at various conferences -- the following is the manuscript from one of these occasions.
Within the theme of this session -- i.e. Mathematics, Skill and Technology -- I have chosen to focus on the question how formalization in general may stimulate and even facilitate invention in technology.
To begin with, let me remind you of the fact that artists often deliberately impose on themselves quite heavy restrictions as to the style and execution of their work. They decide to follow certain rules concerning composition, proportions, the use of figurative elements, a limited selection of colours etc. They regard it as a stimulating challenge to be obliged to work within a minimal repertoire of expressive means. As an example, consider the well-known so called "impossible figures", by the Swedish artist Oskar Reutersvärd. (Figure 1) These drawings are produced in strict adherence to simple formal rules. Each figure is constructed from lines, drawn in only three permitted directions. Because of this, the figure can be interpreted as a solid object, shown in so called axonometric perspective. Following the simple rule you can invent a great variety of figures, most of which are "impossible", in the sense that they cannot be materialized as solid three-dimensional objects. What however makes some of these drawings so fascinating is the fact that if you scrutinize a sufficiently small region of the drawing the oddnes disappears. Locally (that is at each place where the beams meet and are joined together) the object is all right. The "impossibility" is not here or there -- it is something about the object as a whole.
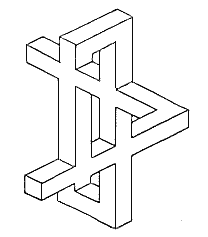 |
Well, this is just one example among many possible ones. It seems evident to me that in art formalization is an important means to stimulate creativity. But of course it is not an end in itself to submit to rules. Rather, real mastery reveals itself in the ability to break a rule, to do the unforeseen at the right moment.
*
Let us now turn to science and technology, where you will find the same inclination to formalize matters in order to stimulate creativity: A multifarious, continuously shifting reality is translated into a system of articulated and relatively invariable elements, which are combined according to given rules. Usually this is done by applying mathematical concepts. The scientist rewrites/redraws the diagrams and formulas in various ways. Then he looks at the result, trying to find out what it implies. The creative use of the formalism is however in no way a trivial matter. A prominent theoretical physicist, Roger Penrose, writes: "It is a mysterious thing in fact how something which looks attractive may have a better chance of being true than something which looks ugly. .. I am sure that successful research workers in practically any field would be familiar with this phenomenon." Thus, to those who really know how to use it, mathematical formalism has an almost magical creative potential. That is why mathematical modelling of a problem can sometimes be so rewarding. And this is also true of formalizing in a more general sense. By giving a clear and transparent structure to the problem, the formalization reveals what is missing, it tells you what further facts you need to be able to solve the problem. I will mention a few examples.
1.
The first example concerns machine construction. Several years ago, during my studies in philosophy, I got to know a man who told me he had invented a "universal construction kit". Experimental working models are used for the purpose of trying out alternative solutions to a mechanical problem. The tentative and flexible character of an experimental model makes it desirable that the material used should permit easy revision of the structure. A universal mechanical construction kit is the ideal instrument for this purpose. Such a kit must have maximum constructive potential within the scope of a reasonable number of parts. So the fundamental concept of my friends invention was the limited number of simple but versatile, high-quality standard components, allowing innumerable combinations thanks to their logical dimensioning and design. Significantly enough the inventor was an artist who was extremely fascinated by the aesthetics of mechanical machinery -- something you can really feel when you look at the photographs in the kit manual. (Figure 2) To him it was self-evident that quality assessment can only be made with the concrete object before ones eyes. One must be able to touch it, hear, smell, manipulate it and watch it working.
 |
Nowadays we use CAD -- Computer Aided Design -- which can be looked upon as a kind of universal construction kit, let be on a higher level of abstraction. The CAD system makes it still more easy to design a model and run a simulation program to see how it will work. You can rapidly study the visual and practical consequences of various changes in the design. By help of advanced computer graphics, you can display variable pictures of the intended object. To be sure, this flexibility and graphicness is stimulating and facilitates invention in several fields of application. But the tentative model you design on the computer is illusory -- it is just a coded description -- and, due to the purely conventional character of this description, the "impossible figure" problem, illustrated by the Reutersvärd drawings, cannot be completely avoided. Furthermore, perception of the object through our senses, so important to my friend, is put aside...
2
Another example is chemical technology. When John Dalton, at the beginning of the nineteenth century, introduced his "New System of Chemical Philosophy" (Figure 3), each symbol represented one atom of an element, and the symbols could be simply joined together to form structures (a few examples of which you can see in the lower part of the picture), representing various chemical compounds.
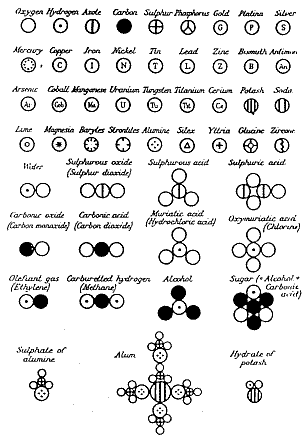 |
Later on the structure-formulas came to be based on the idea of chemical valency. The structure formulas make chemistry into a formalized system, where you reason in terms of various radicals, their geometrical configurations, and the manner in which the structures fit together. Again, formalism facilitates invention in the peculiar game, called "chemical design and synthesis".
3
The electronic revolution is perhaps the most spectacular example of the importance of formalized systems for the growth of technology. Within electronics invention means first and foremost making up new useful combinations of given circuit elements. It relies heavily on tradition, being the continuous exploration of the combinatorial possibilities that certain basic blocks of electronic circuitry possess. From the beginning the elements of this system were the good old resistors, capacitors and inductance coils, together with diodes and transistors. These were soldered together according to a wiring-diagram. Increasing complexity led to new levels of organization. Blocks, consisting of circuits with thousands of basic elements were invented, with strictly specified properties and applicable in various devices. Such blocks (or electronic chips and chip-based subsystems) serve as elementary units at higher levels of the formalized system, the idea being to make each unit as autonomous as possible, so that the interaction between them can be minimized.
Especially with the advent of digital electronics and information technology, this principle of hierarchies within constructions has been carried through with a high degree of sophistication. Probably this is the only conceivable way to handle complexity. By this method you can analyse a problem and design a certain scheme of interactions on an abstract level, without bothering about what has to be going on at lower levels. Each block can be handled as a "black box" as far as its role on the abstract level of systems design is concerned. And each block can be designed independently. A hard-ware description computer language helps to choose the appropriate components at the lower levels. The final implementation in the shape of millions of transistors on a small silicon-plate is done automatically by a program which transforms each block of the invented abstract design into a concrete, detailed circuit.
*
From the examples given above it should be obvious that I speak of "formalized systems" in the broadest application of the term. The issue to be discussed is to what extent the formalization of a theoretical or practical activity stimulates inventiveness. I think that invention is facilitated by the survey of the problem that a formalized system makes possible. Undoubtedly the repertoire is narrowed down and becomes more specific. It is certainly true that any CAD program has its limitations. And yet its potential seems inexhaustible. Formalism becomes the needle's eye that an idea has to pass through.
Moreover, inventions are conceived on two levels. The first level is within the framework of the formalized system, and consists in the exploration of the systems possibilities. The second level is reached when one deliberately goes outside the system, designing fundamentally new elements. Sometimes even using new physical phenomena. Such innovations are relatively rare but lead, when implemented, to explosive development. The point I want to make is that fruitful innovations might appear as the result of acceptance as well as denial of the formalized system -- as the case may be. In both cases creativity is stimulated by the very existence of a formal system, tentatively describing the field of inquiry in a distinct and well-articulated way.
So far, so good. Every coin, however, has two sides. It would not be fair, if we did not consider the thesis at issue from quite the opposite point of view, questioning the usefulness of formalizing. Could it not equally well be the case that the adherence to strict rules and concepts, together with a routinely employed symbolic calculus, would sooner hamper creativity and rather prevent than facilitate inventions? In science innovation means to come up with new instruments, find new ways to approach the given reality. How could inventiveness ever feel at home within an established symbolic framework? A formalized system makes you see some things exactly by preventing you from seeing others! It is only by being informal, not slavishly following the established routes, that you can ever hope to find something radically new.
It cannot be denied that such objections must be taken seriously. I see no other solution to this evident dilemma than to underline that we should never permit ourselves to be slaves under the formulas and rules we use in calculating and planning things. We must always be prepared to break the rules, give up habits, and find new rules. Transcend the momentary borders of scientific practice. This amounts to an attitude of playfulness. But it must be done with keen discernment. You must know what you are doing, you must be the master of your formulas, your symbolic games -- not their slave! Just to play around with formulas and diagrams does not result in true inventions. To be a good systems designer you must use your intuition. You must be intimately familiar with the realities that your analysis concerns. The formulas "tell" you something, but it is you, the conscious user of the symbolism, who judges whether what the formulas tell you is valuable or not. We must beware of designing "impossible objects" without knowing that we do it!
© Pehr Sällström 1995 and 2006, creative.htm at http://pscolour.eu